
Prove That X Y Z Xy Yz Zx Is Always Positive Mathematics Topperlearning Com 58pxibcc
3dprinting, solidworks f(0,0,0) is 0, not 1 (the isosurface level), so you only get points drawn completing the cones if there are enough points near the origin that happen to have value 1 But when you switch to linspace(,,), the closest coordinates to the origin are at about 105, leaving a gap of about 21F(x y z) = (xyz)(xy'z)(xy'z')(x'yz')(x'y'z) = ΠM(0, 2, 3, 5, 6) Note that the Minterm List and Maxterm List taken together include the number of every row of the Truth Table That means that if you determine either one of the lists, you can determine
(x^2-y^2)^3 (y^2-z^2)^3 (z^2-x^2)^3/(x-y)^3 (y-z)^3 (z-x)^3
(x^2-y^2)^3 (y^2-z^2)^3 (z^2-x^2)^3/(x-y)^3 (y-z)^3 (z-x)^3-The system displayed follows the righthand ruleIf we take our right hand and align the fingers with the positive xaxis, then curl the fingers so they point inThere are no solutions The original equation, considered by Markov, was $$ x^2 y^2 z^2 = 3xyz $$ This leads to the Markov Numbers Adolf Hurwitz considered such equations in three or more variables, in 1907
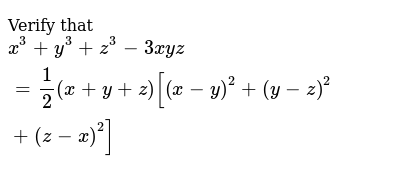
Verify That X 3 Y 3 Z 3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2
Answer by You can put this solution on YOUR website!Given, x^2y^2z^2=2 (xyz)3=2*x2*y2*z3 or, x^2–2*xy^22*yz^22*z=3=1–1–1 or,x (x2)y (y2)z (z2)=1–1–1 Now let us assume, x (x2)=1>x^2*x1=0> (x1)^2=0, or, x=1 y (y2)=1>y^22*y1=0> (y1)^2=0, or y=1 z (z2)=1>z^22*z1=0> (z1)^2=0, or,z=1Use substitution to solve for x and y And they give us a system of equations here y is equal to negative 5x plus 8 and 10x plus 2y is equal to negative 2 So they've set it up for us pretty well They already have y explicitly solved for up here So they tell us, this first constraint tells us that y must be equal to negative 5x plus 8
8x y z = 9, 2x 2y 3z = 22 and x 3y 2z = 15 solve for an ordered tripple asked in ALGEBRA 2 by harvy0496 Apprentice systemofequationsSimplify (X^2 Y^2)^3 (Y^2 Z^2)^3 (Z^2 X^2)^3/(X Y)^3 (Y Z)^3 (Z X)^3 CISCE ICSE Class 9 Question Papers 10 Textbook Solutions Important Solutions 6 Question Bank Solutions Concept Notes & Videos 431 Syllabus Advertisement Ex 32, 12 Given 3 8(x&y@z&w) = 8(x&6@−1&2w) 8(4&xy@zw&3) find the values of x, y, z and w 3 8(x&y@z&w) = 8(x&6@−1&2w) 8(4&xy@zw&3) 8
(x^2-y^2)^3 (y^2-z^2)^3 (z^2-x^2)^3/(x-y)^3 (y-z)^3 (z-x)^3のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
 A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
 A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
 A15 Rb30 Rc40 Rd48 R 15 R30 R48 | 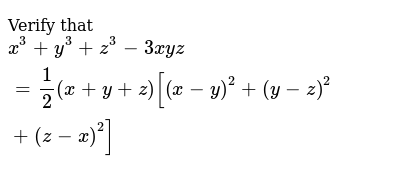 A15 Rb30 Rc40 Rd48 R 15 R30 R48 | A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
 A15 Rb30 Rc40 Rd48 R 15 R30 R48 | 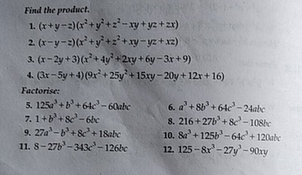 A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
 A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
 A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 | 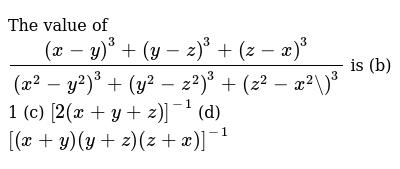 A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
 A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
 A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
A15 Rb30 Rc40 Rd48 R 15 R30 R48 | A15 Rb30 Rc40 Rd48 R 15 R30 R48 | A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
 A15 Rb30 Rc40 Rd48 R 15 R30 R48 | 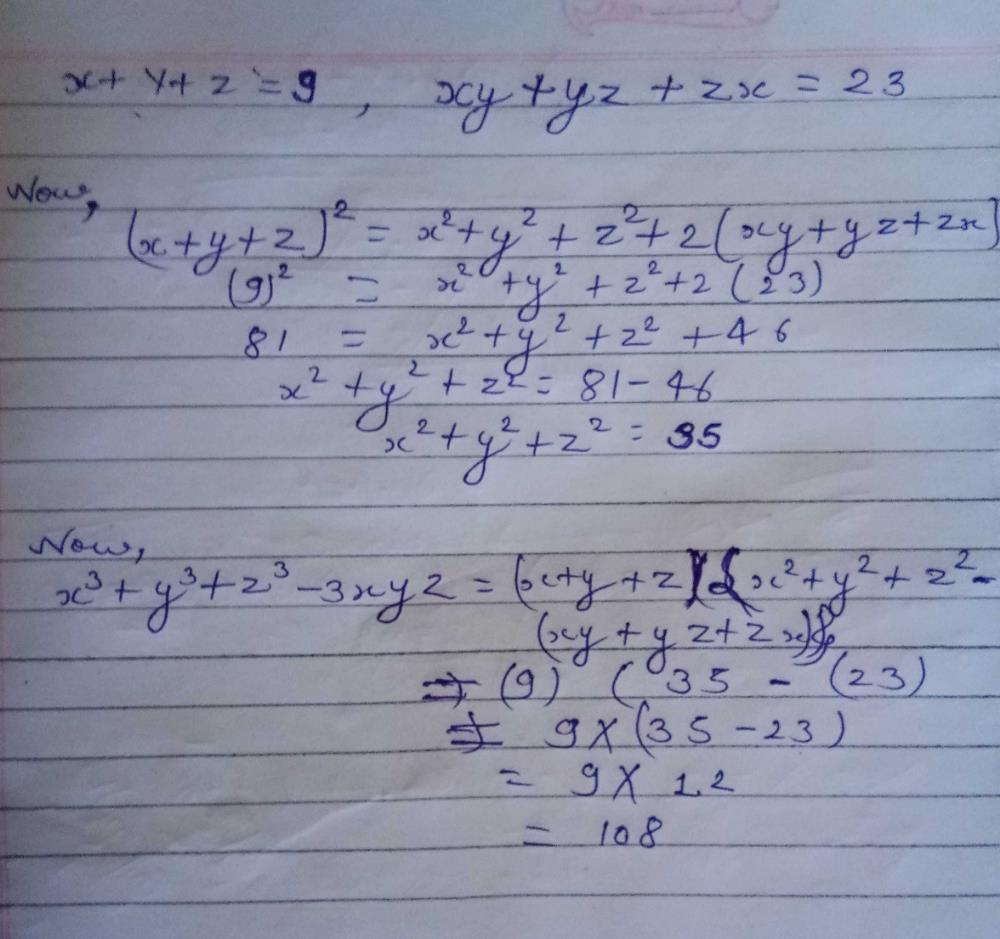 A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
 A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 | A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
 A15 Rb30 Rc40 Rd48 R 15 R30 R48 | 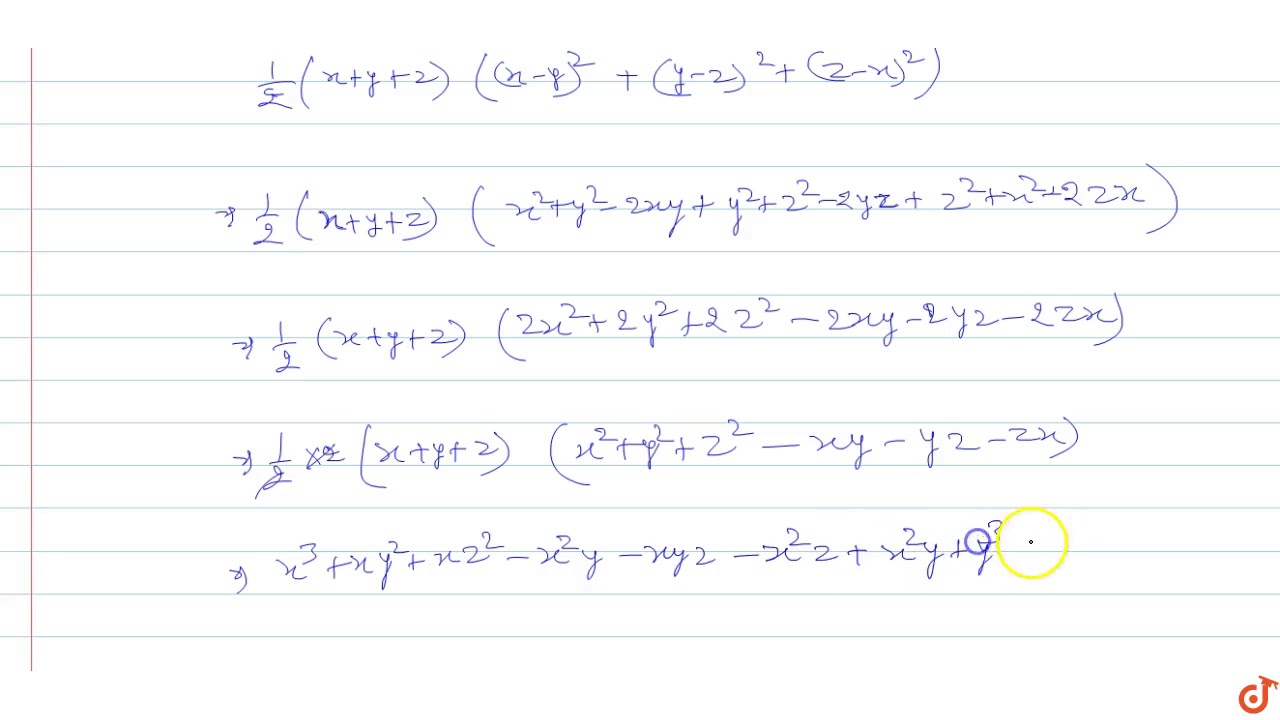 A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
 A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 | A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
A15 Rb30 Rc40 Rd48 R 15 R30 R48 | A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
 A15 Rb30 Rc40 Rd48 R 15 R30 R48 | A15 Rb30 Rc40 Rd48 R 15 R30 R48 | 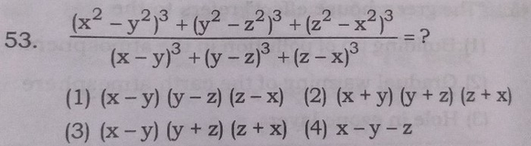 A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
 A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
A15 Rb30 Rc40 Rd48 R 15 R30 R48 | A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
 A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 | A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
 A15 Rb30 Rc40 Rd48 R 15 R30 R48 | A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
 A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 | A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
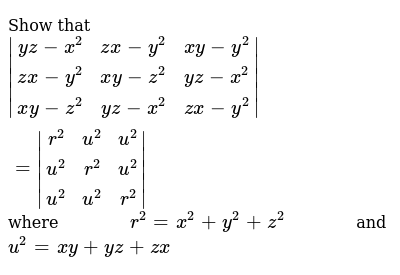 A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 | A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
 A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
 A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
 A15 Rb30 Rc40 Rd48 R 15 R30 R48 | A15 Rb30 Rc40 Rd48 R 15 R30 R48 | A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 | A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
A15 Rb30 Rc40 Rd48 R 15 R30 R48 | 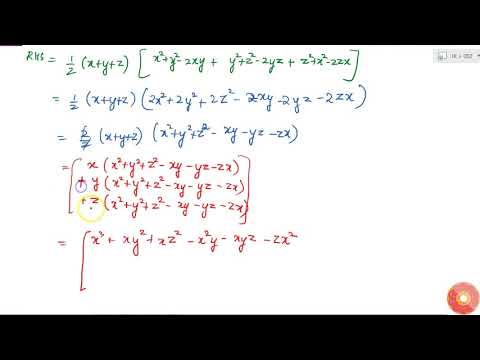 A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
A15 Rb30 Rc40 Rd48 R 15 R30 R48 | 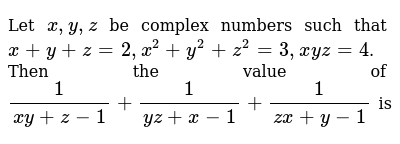 A15 Rb30 Rc40 Rd48 R 15 R30 R48 |  A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
 A15 Rb30 Rc40 Rd48 R 15 R30 R48 | A15 Rb30 Rc40 Rd48 R 15 R30 R48 | A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
 A15 Rb30 Rc40 Rd48 R 15 R30 R48 | 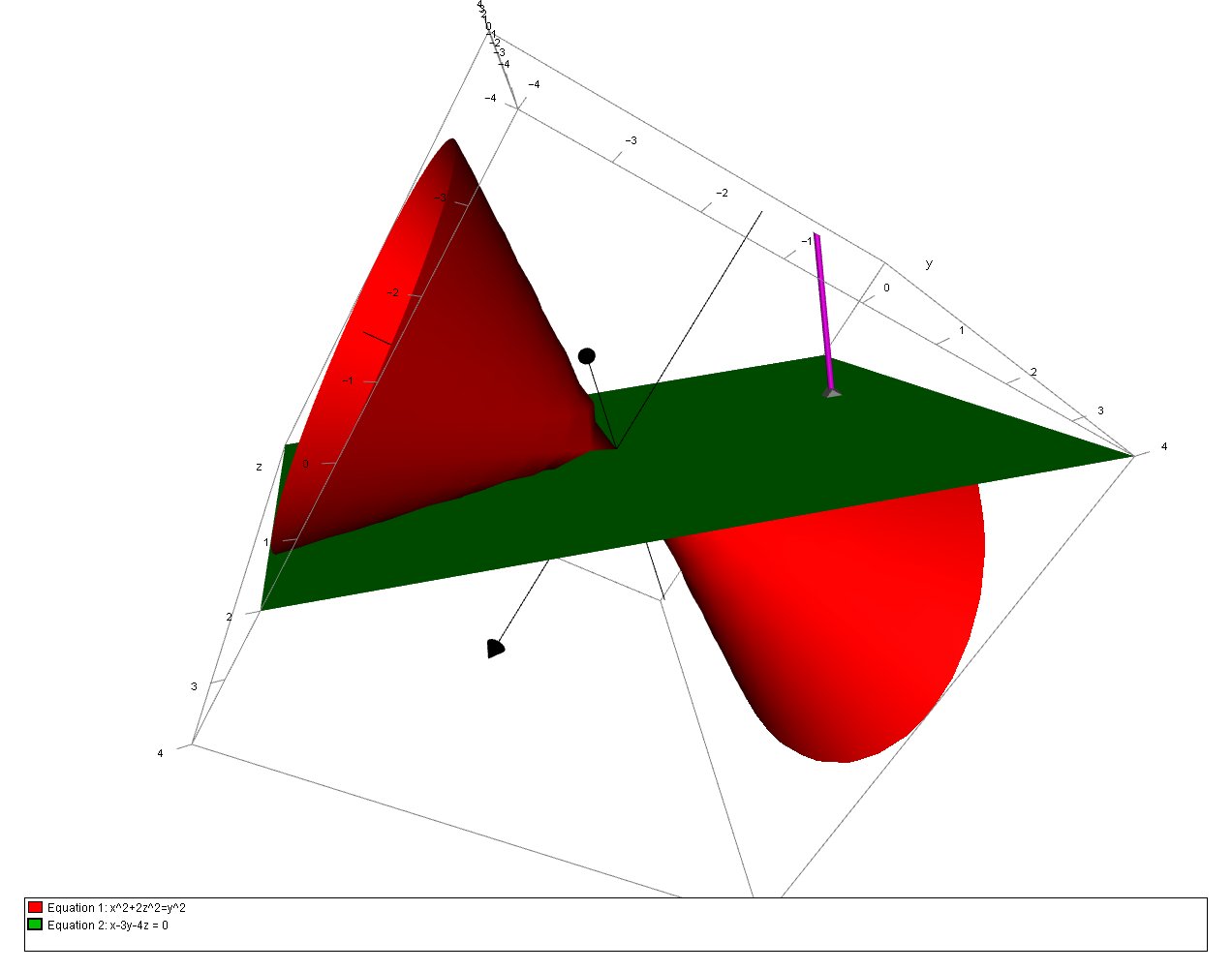 A15 Rb30 Rc40 Rd48 R 15 R30 R48 |
WolframAlpha Computational Intelligence Natural Language Math Input NEW Use textbook math notation to enter your math Try it × Extended Keyboard Examples Compute expertlevel answers using Wolfram's breakthrough algorithms, knowledgebase and AI technologyThis integral of a function along a curve C is often written in abbreviated form as ∫ C f ( x, y) d s Example 1621 Compute ∫ C y e x d s where C is the line segment from ( 1, 2) to ( 4, 7) We write the line segment as a vector function r = 1, 2 t 3, 5 , 0 ≤ t





0 件のコメント:
コメントを投稿